구간 합은 합 배열이라는 것을 이용하여 시간 복잡도를 줄이는 알고리즘이다.
코딩 테스트에서는 사용 빈도가 높다고 한다.
핵심 이론
구간 합 알고리즘을 활용하려면 먼저 합 배열을 구해야 한다.
배열 A가 있을 대 합 배열 S는 아래와 같이 정의할 수 있다.
S[i] = A[0] + A[1] + A[2] + ... + A[i-1] + A[i] // A[0]부터 A[i]까지의 합
합 배열은 기존의 배열을 전처리한 배열이다.
합 배열을 미리 구해 놓으면 일정 범위의 합을 구하는 시간 복잡도가 줄어든다.
어떻게 줄어드나요?
--> O(N)에서 O(1)이라는 선형 시간으로 줄어들게 됩니다 :)
A[i]부터 A[j]까지의 배열 합을 합 배열 없이 구하는 경우,
최악의 경우를 생각해보자.
i가 0이고 j가 N인 경우일 것이고, 시간 복잡도는 O(N)이다.
합 배열은 아래와 같은 간단한 공식으로 표현 가능하다.
S[i] = S[i-1] + A[i]
위의 식을 활용하며 합 배열을 이용하여 쉽게 구현 가능하다.
아래는 i에서 j까지 구간 합을 구하는 공식이다.
S[j] - S[i-1] // i에서 j까지 구간 합
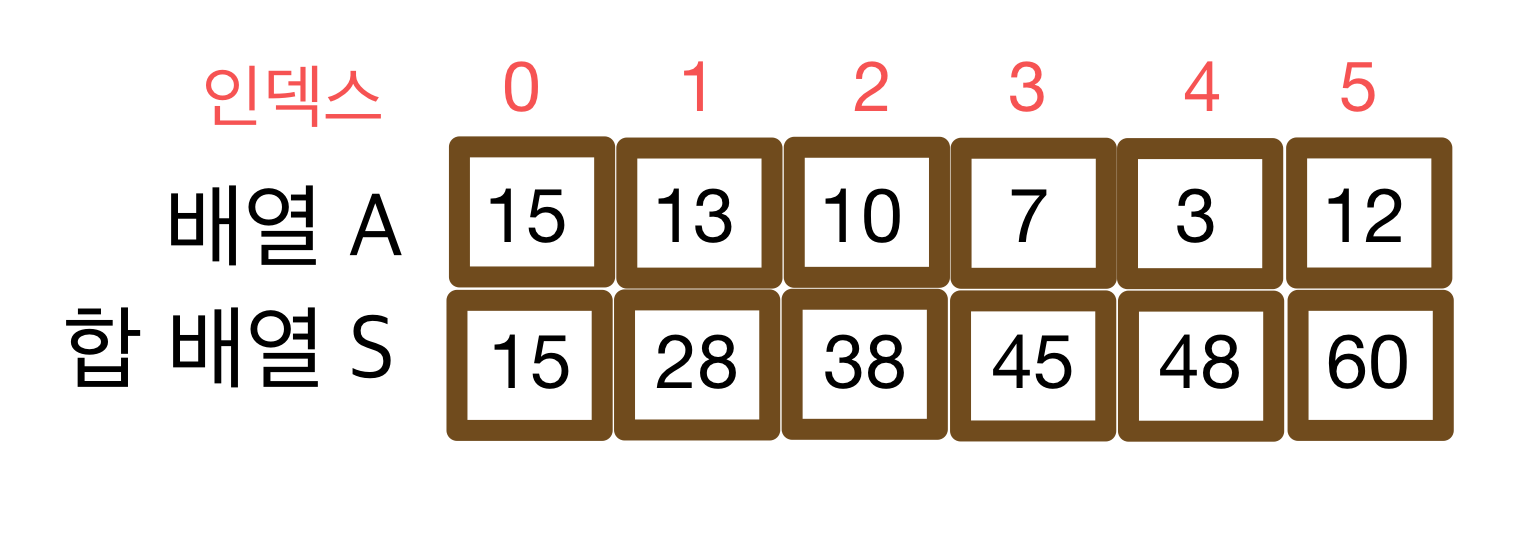
구간 합 공식을 아래의 그림으로 예시와 함께 설명하겠다.

그림에서 알 수 있듯이 합 배열과 구간 합은 연관되어 있다.
A[0] + ... + A[5]에서 A[0] + A[1]을 제외하면(빼면)
구간 합 A[2] + ... + A[5] 가 나오기 때문에
결론 !!
S[5]에서 S[1]을 빼면 구간 합을 쉽게 구할 수 있다.
(=합 배열을 미리 구해 두면 구간 합은 한 번의 연산으로 구할 수 있다)
A[2] ~ A[5] 구간 합을 합 배열로 구하는 과정을 알아보자.
S[5] = A[0] + A[1] + A[2] + A[3] + A[4] + A[5]
S[1] = A[0] + A[1]
S[5] - S[1] = A[2] + A[3] + A[4] + A[5]
합 배열과 구간 합 공식을 잘 활용하여
시간 복잡도를 줄여보자.
'Algorithm' 카테고리의 다른 글
| [백준] 11660번 : 구간 합 구하기 5 - C/C++ (0) | 2025.03.11 |
|---|---|
| [백준] 11659번 : 구간 합 구하기 4 - C/C++ (0) | 2025.03.07 |
| [백준] 10867번 : 중복 빼고 정렬하기 - C/C++ (0) | 2025.03.06 |
| [백준] 2493번 : 탑 - C/C++ (0) | 2025.03.06 |
| [백준] 1546번 : 평균 - C/C++ (0) | 2025.03.05 |



