
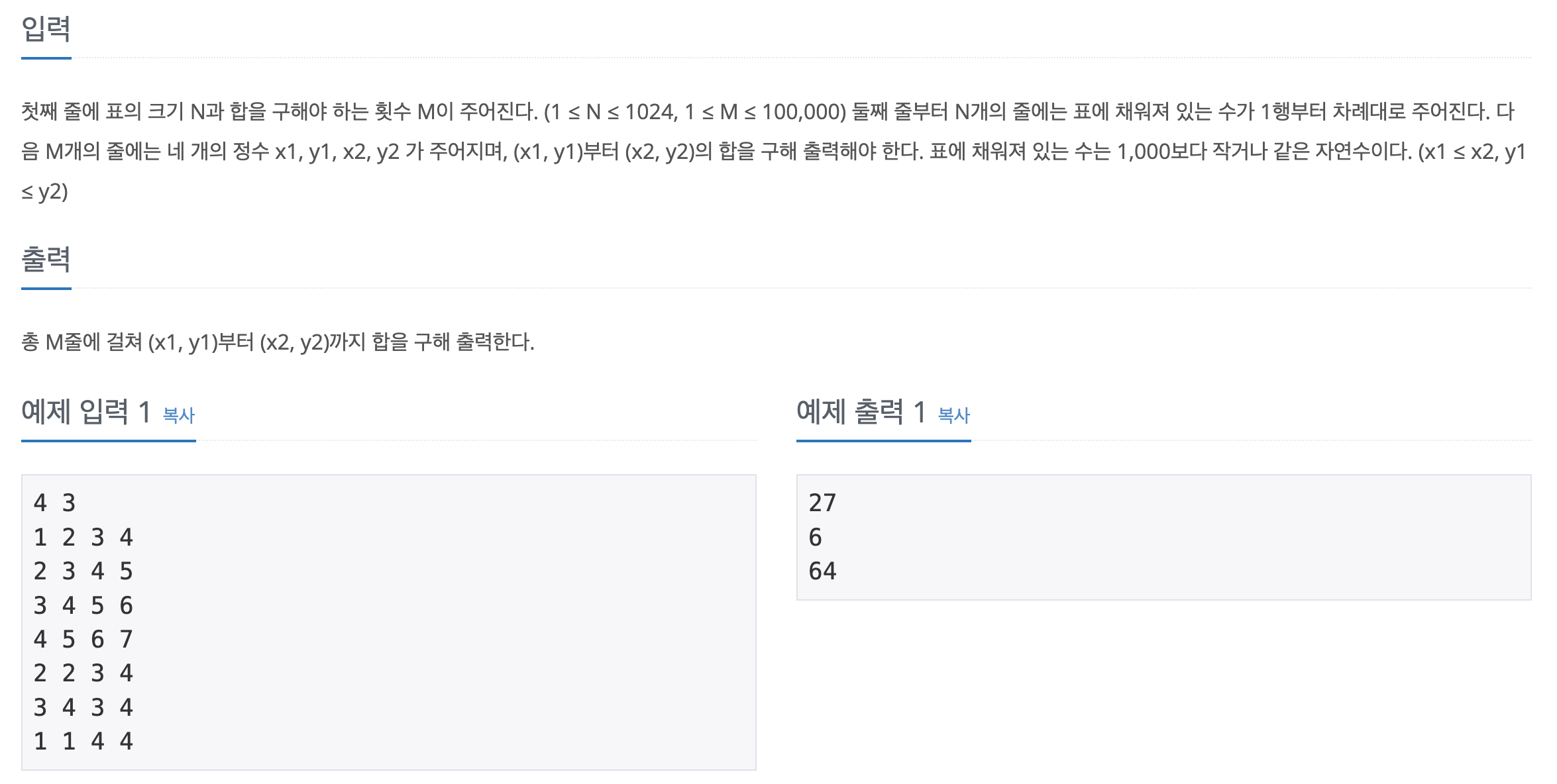

지난번에 풀었던 문제와 비슷하다.
누적합(prefix sum)을 이용하자.
입력 받은 2차원 배열을 저장할 공간과 누적합을 저장할 dp 테이블을 미리 선언해주자.
int sum[1025][1025], dp[1025][1025];
N과 M을 입력 받았다면 dp를 처리하자.
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
cin >> sum[i][j];
dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + sum[i][j];
}
}
왜 dp를 저렇게 처리하나요?
https://binaryroot.tistory.com/17
[자료구조] 구간 합
구간 합은 합 배열이라는 것을 이용하여 시간 복잡도를 줄이는 알고리즘이다.코딩 테스트에서는 사용 빈도가 높다고 한다. 핵심 이론구간 합 알고리즘을 활용하려면 먼저 합 배열을 구해야 한
binaryroot.tistory.com
위의 링크에 정리해두었지만,
한 번 더 설명하겠다.
dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + sum[i][j]
위에서 사용한 코드는 현재 위치까지의 사각형 합을 저장하는 공식이다.
이전까지의 누적합을 활용하는 것이다.
누적합이면 더하기만 해야지, 왜 빼요?
--> 두 번 제거된 것이 있을 수 있으니, 중복 계산을 피하기 위함입니다.
dp를 처리했다면, 이제 구간 합을 구할 차례이다.
문제에서 요구하는 (x1, y1)부터 (x2, y2)까지의 부분 합(구간 합)을 구하자.
구간 합 공식을 알아보자.
prefix = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]
- dp[x2][y2]는 dp의 전체 합을 의미한다.
- - dp[x1-1][y2]: 위쪽 불필요한 부분 제거
- - dp[x2][y1-1]: 왼쪽 불필요한 부분 제거
- + dp[x1-1][y1-1]: 위쪽과 왼쪽에서 중복 제거된 부분 복구
for(int i = 0; i < m; i++){
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
prefix = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1];
cout << prefix << '\n';
}
코드로 표현하면 위와 같다.
해당 문제를 풀기 위해서 우리가 알아야하는 개념은 다음과 같다.
- 누적 합(prefix sum)
- 2차원 배열 합 구하기
- dp
전체 코드
#include <iostream>
//구간 합 구하기5
using namespace std;
int sum[1025][1025],dp[1025][1025];
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n,m;
cin >> n >> m;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
cin >> sum[i][j];
dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + sum[i][j];
}
}
int prefix;
for(int i = 0; i < m; i++){
int x1,y1,x2,y2;
cin >> x1 >> y1;
cin >> x2 >> y2;
prefix = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1];
cout << prefix << '\n';
}
return 0;
}
난이도 실버1의 문제였다.
코드를 쓰는 것도 어려운데, 이 알고리즘을 풀기 위해서 필요한 개념은 더 어렵게 느껴지는 것 같다.
알고리즘 문제를 해결할 때 dp가 중요하다고는 많이 듣고 다양한 문제를 보긴 했지만,
나에게는 아직 너무 어려운 것 같다.
하나하나 차근차근 공부하는 것이 나에게 맞는 것 같기도 하다.
더 좋은 풀이가 있다면 댓글로 알려주세요 !!
피드백 환영입니다☺️
'Algorithm' 카테고리의 다른 글
| [백준] 2839번 : 설탕 배달 - C/C++ (0) | 2025.03.13 |
|---|---|
| [백준] 1292번 : 쉽게 푸는 문제 - C/C++ (0) | 2025.03.11 |
| [백준] 11659번 : 구간 합 구하기 4 - C/C++ (0) | 2025.03.07 |
| [자료구조] 구간 합 (0) | 2025.03.07 |
| [백준] 10867번 : 중복 빼고 정렬하기 - C/C++ (0) | 2025.03.06 |



